Teaching Techniques of Integration, Part 3

This is the breakdown of class time by content for the second quarter course on analytic geometry and calculus (primarily intended for engineering students) that I am teaching this quarter.

It follows the required text: Stewart’s Calculus, which is one of the best selling textbooks on Calculus in the US and Canada at the university, college, and high school levels.  As such, this break down is probably fairly typical.

The finer breakdown of the two major categories is:

Applications of Integration	Techniques of Integration
Areas between curves	Substitution
Volumes by cross section	Integration by parts
Volumes of revolution by shells	Trigonometric Integrals
Work	Trigonometric Substitution
Average Value of a function	Partial Fractions
Arc length	Tables and Computer Algebra Systems

The main point of my previous two posts was to ask the question of whether it is time to tone down the emphasis on rote computations for computing formulas for antiderivatives in terms of elementary functions (the utility of which is to set up equations and solve practical problems) in favor of teaching alternative methods for such problem solving that apply concepts and utilize readily available electronic tools.  From the comments I received (here and elsewhere), this appears to be a rather polarizing issue.  Several readers missed my careful choice of words and responded as though I was advocating removing the “techniques of integration” pie piece completely from the curriculum.  Others championed such a move, possibly with caveats for including some of the techniques but not all.

My question is really more nuanced.  It’s about making strategic decisions on coverage in course design so as to deliver the highest quality course to the students I have now.  I’m asking: is it really of benefit to this generation of calculus students to spend 31% of a course on one particular method of problem solving?  What about the next generation?  Instead of 31% vs. 0%, should it be more like 21% vs. 10% now and maybe 10% vs. 21% ten years from now?  Of course, any such scale must be adjusted to the local audience.

Praise for emphasizing Rote Integral Computations

• Problem solving confidence builds with successful completion of such computations.
• Pencil and paper computations can have the effect of “making the theory real.”
• It feels like a payoff for years of training in algebra and trigonometry.
• Makes improper integrals of varying degrees of complexity, accessible and possible to analyze.
• Ability to successfully execute the algorithms for such computations makes you feel smart.
• Practice with such computations teaches you to pay attention to details.
• Many integrals that arise in the application of calculus (like can be calculated using well practiced techniques faster than they can be manually entered and evaluated by computer.
• Develops the ability to re-derive and verify integral table entries and formulas that are available for reference (especially those available from unrefereed sources).

Criticism for emphasizing Rote Integral Computations

• Problem solving confidence is stifled with repeated failure at execution of such computations.
• Emphasis on computations of this sort can make concepts opaque.  How many students think that the definition of is the symbols ?
• This is sometimes offered as the main goal for learning algebra and trigonometry.
• It substantiates the belief that is meaningless/worthless unless you can find a formula for a so that you can write down .
• Inability to execute such computations can make you feel not smart.  How many students do we lose in calculus courses because they have difficulty completing the algebraic/trigonometric aspects of such computations?
• Many integrals that arise in the application of calculus (like from the great fuel tank problem) can not be calculated using well practiced techniques faster than they can be manually entered and evaluated by a computer.

There are clearly important benefits and drawbacks, with sound points on either side.  This debate reminds me of the Laffer Curve from economics.  Suppose that you could determine a country’s production from its income tax rate.  If you believe such a function exists and is differentiable, then the curve might look like this:

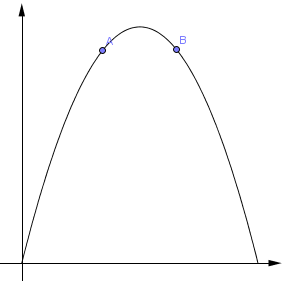where the horizontal axis is the tax rate and the vertical axis is production. Indeed, if the government collects no taxes, there is no revenue for infrastructure to support trade (roads, water treatment, currency, etc) and thus no production.  Likewise, if the government taxes at a rate of 100%, then no commerce can be done, so nothing will be produced.  Yet, it is non-negative function which, by observation, we know to be positive at some rate in between, so the curve must have horizontal tangent somewhere in between (Rolle’s Theorem).  The progressive/liberal argument is that we are always at position A.  With slightly more taxation, we could provide better support of trade and increase productivity.  The conservative argument is that we are always at position B.  By cutting taxes, we could free up funds to be used more effectively by businesses to increase productivity.

In the case of our debate, however, the roles seem to be reversed.  If the horizontal axis corresponds to emphasis (percentage of class time) on rote techniques of integration in an integral calculus course and the vertical axis corresponds to production of problem solvers then the progressive and conservative standpoints are switched.  The conservative argument is that we are at position A.  If we focus more on rote techniques and pencil and paper methods we will we will be more effective in producing masters of calculus skills and therefore more effective at producing problem solvers.  The progressive argument is that we are at position B.  If we focus less on rote techniques and pencil and paper methods, the benefits are that we can spend more time training a diversity of problem solving techniques and more effectively produce problem solvers.

Personally, I think we are at position B.   I see focusing heavily on rote techniques of integration as coming at a substantial price.  There is a technological sea change occurring in world culture and I think it having the effect of shifting the peak to the left, making emphasis at B less and less effective.  By focusing heavily on mechanical calculations we are ignoring the pivotal role that conceptual understanding and analytic reasoning using readily available tools will have in the future application of calculus and the training of effective problem solvers.